How many bits are your ears? What is the difference in sound quality due to the number of quantization bits?
I did not find a good homepage even if I searched on the web for a while, so I decided to make it myself.
(I can find a lot of mosquito sound comparisons …)
It is “On the effect of quantization bit number on sound quality”.
The quantization bit number is a value that indicates at what stage music source information is expressed. The higher the value, the more faithful the sound source is.
For example, if the quantization bit number is 8 bits, it is possible to represent a number between -128 and +127 in binary, and if it is 16 bits, it is possible to represent a value between -32768 and +32767. I can do it.
Recently, high-resolution sound sources have become a hot topic, but most of the high-resolution sound sources that are said to have “good sound” have 24 bits of quantization.
CD quantization bit number is 16 bits
Nostalgic family computers are less than 8 bits.
If the number of quantization bits increases by 1 bit, the amount of information will be doubled, so compared to 8 bits of old game machines
Since the high-resolution sound source is [24bit-8bit = 16bit], it contains 2 16 (65535) times more detailed information.
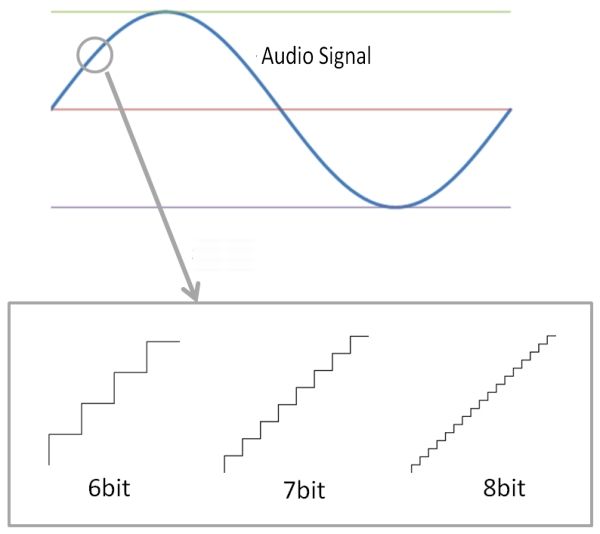
As the number of quantization bits increases, the jerky waveform becomes smoother and closer to the original sound.
Even if you can imagine that the higher the number of bits, the better the sound in the head, I think that there are not so many people who have heard the difference.
Therefore, this time, let’s compare the difference in the number of quantization bids with the actual sound.
Below we have prepared a WAV file in 2bit increments from 4bit to 16bit.
Note) WAV files can be played only on browsers that can play them. If you don’t support the environment, you’re sorry.
Let’s compare and hear the sounds with different number of quantization bits.
e.g. 1) First, it is a sinusoidal waveform of 1 kHz which is easy to understand and well standardized for sound.
A: 1 kHz sine wave (quantization bit number = 4 bits)
B: 1 kHz sine wave (quantization bit number = 6 bits)
C: 1 kHz sine wave (quantization bit number = 8 bits)
D: 1 kHz sine wave (quantization bit number = 10 bits)
E: 1 kHz sine wave (quantization bit number = 12 bits)
F: 1 kHz sine wave (quantization bit number = 14 bits)
G: 1 kHz sine wave (quantization bit number = 16 bits CD quality)
How is it? I do not understand the difference beyond a certain bit.
e.g. 2) Next is the intro of Mozart’s “Eine kleine Nachtmusik”.
A: Mozart (quantization bit number = 4 bits)
B: Mozart (quantization bit number = 6 bits)
C: Mozart (quantization bit number = 8 bits)
D: Mozart (quantization bit number = 10 bits)
E: Mozart (quantization bit number = 12 bits)
F: Mozart (quantization bit number = 14 bits)
G: Mozart (quantization bit number = 16 bits CD quality)
Oh? After all, do you lose confidence in hearing the difference from a certain number of bids?
Then do you need a high-resolution sound source?
I think there are people who just listen to this and don’t need high res, but it’s not really that simple.
The above WAV file has been adjusted so that the maximum volume is 0dB (maximum output volume).
In the case of an 8-bit SIN waveform, the peak above the peak is +127. The peak below the mountain is -128.
What happens if the volume of this SIN waveform is halved?
The peak above the mountain is +63. The peak below the mountain is -64. This is the same waveform as the 7-bit SIN waveform.
If the volume is further halved, the peak above the mountain is +31. The peak below the mountain is -32, which is the same as the 6-bit SIN waveform.
So, the lower the volume at the time of recording, the smaller the apparent number of quantization bits.
In the case of CDs, the resolution which is originally 16 bits is actually worse at 15 or 14 bits for poor recording.
This phenomenon is more pronounced in orchestral performances. In the case of an orchestra, the difference between loud and loud parts is generally very large. There are plenty of scenes that can only be heard if you listen carefully, such as the parts played in pianissimo.
In such a case, the larger the number of quantization bits, the better. For example, if the volume difference between a scene played by an orchestra in fortissimo and a scene played in pianissimo is about 200 times (46 dB), in the case of a 16-bit CD, the pianissimo part will have an apparent quantization bit number of half, 8 It will be a bit.
If this is a high-resolution sound source, even if the volume is reduced from 24 bits by 200 times (46 dB), the quantization bit number for 16 bits is still secured, so the sound does not feel bad.
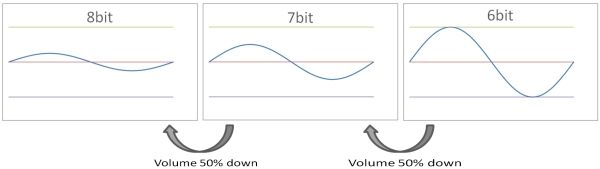
The above waveforms all have the same sound quality. Even if there is an 8-bit quantization bit rate, if the volume is set to 25%, the apparent 6-bit quantization bit rate will result.
To summarize the above
- Before talking about the number of quantization bits, the recording needs to be in the best condition. (Must be a recording worthy of comparison)
- Both CD and high-resolution sound sources do not change much where the volume is high. (I don’t understand the difference between the sounds)
- Since the apparent number of quantization bits decreases at a very low volume, a high-resolution sound source with a large number of quantization bits is by far the most advantageous. (I personally think this makes a big difference)
Why does it sound reasonable even with a low quantization bit?
We can hear unexpectedly 8bit sound. It’s a little strange what the resolution is even though it has only 256 resolutions.
By the way, could you distinguish between a sound with a low quantization bit rate and a sound with a high bit number in terms of sound quality?
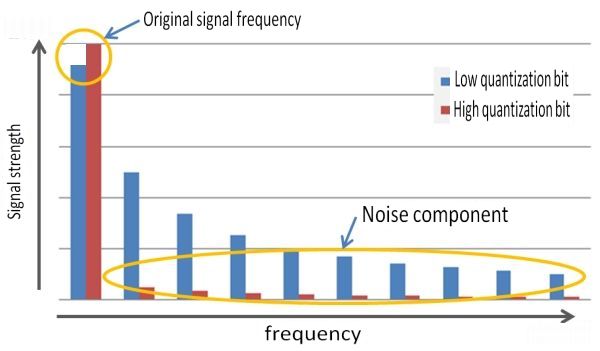
In fact, the noise level on the treble side is different. This can be clearly seen by looking at the frequency spectra of a sound with a large number of quantization bits (a waveform close to the original sound) and a sound with a small number of quantization bits (a wavy and step-like waveform).
As the number of quantization bits decreases, a spectrum appears on the higher tone (higher frequency) side. This is audible as “sir” or “bee” noise. Even if the number of quantization bits is reduced, the basic sound itself does not change.
The ear itself acts as a filter, so it sounds reasonable
In this WAV file sample example, the SIN waveform was 1kHz.
In this case, 2kHz, 3kHz, 4kHz …. and 1kHz harmonics can be heard as noise.
What if this is a 10kHz SIN wave? Harmonics above 10kHz are 20kHz, so you can’t hear them in the first place. (Except those who can hear the 20kHz mosquito sound)
In fact, the ear has a very steep filter characteristic and can only hear a very narrow range of sounds. Especially as you age, the range gets smaller and smaller. (By the way, I can only hear the sound up to 13kHz) It is the result of compensating for the low quantization bit.
* If you want to find out what frequency you can hear, you can find a lot by searching for “mosquito sound”.
Summary
Probably in the case of easy listening such as BGM, high-resolution sound source is probably unnecessary. Because, in most cases, the noise in the room is louder than the noise caused by low quantization bits (generally called quantization noise).
However, if you want to listen to music seriously, you still want a high-resolution sound source. It is especially recommended when there is a large difference between a loud sound and a small sound, such as an orchestra, because the difference is likely to occur. However, keep in mind that it is limited to sound recordings.